Calculation Of Force Based On Newton's Second Law Of Motion (3) 

Question 1.

A block of mass 2.0 kg resting on a smooth horizontal plane is acted upon simultaneously by two forces, 10 N due North and 10 N due East. The magnitude of the acceleration produced by the forces on the block is?

Solution:

Using the formula for force, F = ma

Given, force = ?, mass = 2.0 kg, acceleration = ?

First, find the net force of the two acting on the mass.

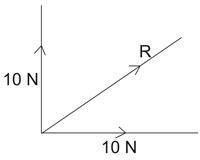
Using pythagora’s theorem, the resultant force, R is given as R² = 10² + 10²

 R  = √(102 + 102)    =  √200  = 14.4 N

 Applying the net force to the force formula, 

 F = ma

 14.14 = 2.0 x a

a = ^14.14/₂ = 7.07 m/s²

Question 2.

A 0.05kg bullet travelling at 500 ms-1 horizontally strikes a thick vertical wall. It stops after penetrating through the wall a horizontal distance of 0.25 m. What is the magnitude of the average force the wall exerts on the bullet?

Solution:

The force the wall exerted on the bullet in bringing it to rest or stop equals the force the bullet was travelling with.

Using the formula for force, F = ma

Given: mass = 0.05 kg, initial velocity u = 500 ms^-1, final velocity v = 0, distance travelled = 0.25 m, acceleration = ?

To find the acceleration of the bullet, use the equation of motion,

v² = u² + 2as, where v = final velocity, u = initial velocity,     a = acceleration, s = distance moved.

Therefore, from the equation of motion,

a = (v² – u²)/2s  

substituting (^{v2 – u2}/_2s ) for a in the force equation, we have

F = m (^{v2 – u2}/_2s)

 F = 0.05 ((0 – 500²)/2 x 0.25)

   = 25 000 N

 The force the wall exerted on the bullet is 25 000 Newtons.

Question 3.

When taking a penalty kick, a footballer applies a force of 30.0 N for a period of 0.05s. If the mass of the ball is 0.075 kg, calculate the speed with which the ball moves off.

Solution:

Using the formula for force,

F = m (^{v – u}/_t)

Given: Force = 30 N, mass = 0.075 kg, initial velocity,   u = 0, final velocity, v = ?, time t = 0.05 s

 Therefore, with the above force formula,

 30 = 0.075 (^{v – 0}/_0.05)

 0.075 v = 30 x 0.05

v = ^{30 x 0.05}/_0.075 = 20

The speed (or velocity with which the ball moves off is  20 m/s

Question 4.

A body of mass 2 kg moving vertically upwards has its    velocity increased uniformly from 10 ms^-1 to 40 ms^-1 in 4s. Neglecting air resistance, calculate the upward vertical force acting on the body, taking acceleration due to gravity as 10 ms^-2.

Solution:

Neglecting air resistance, two forces act on the body as it moves upwards: (1) the upward vertical force, F, and (2) the downward force due to gravity, mg.

The net force is the difference between the two forces.

 i.e.

 F – mg = ma

 F = ma + mg

 F = m (a + g)

 Notice that  a = ∆v/t 

                       = ^{v – u}/_t   

                        = ^{40 – 10}/ ₄

                       = 30/4 = 7.5 ms^-2

 Therefore, from

F = m (a + g)

F = 2 (7.5 + 10)

F = 2 x 17.5

F = 35 N

The upward vertical force acting on the body is 35 Newtons

Question 5.

A force on a body causes a change in the momentum of the body from 12 kgms^-1 to 16 kgms^-1 in 0.2s. Calculate the magnitude of the impulse.

Solution:

From Newton’s second law of motion

 F = ^{(mv – mu)}/_t

 Ft = mv – mu

 Ft = Impulse (I)

 Therefore, I = mv – mu

 Where mv = final momentum, mu = initial momentum.

 I = 16 – 12 = 4 Ns

See calculations of force based on Newton's second law of motion (4) here.